Algo
A gentle introduction to algorithms.
Big O
"Big O" is a notation used to classify algorithm space ( memory ) and time requirement. It expresses how those requirements will grow relative to the input size.
In other words, if the input would be twice - or ten times - as big, how much longer would the function take to run, and how much more memory would it need.
Let's take the example of running an algorithm first with an input of size 10 and then a second tine with an input of size 100, and look at the most common big O classes and what they mean for those two input size. We'll call the difference between the two run times delta, where the run time for the first input is our base at 1, and the run time for the second input is how much longer it would need to run for processing the input that's 100 time bigger.
| Big O | Name | Delta | Examples |
|---|---|---|---|
| O(1) | Constant | Same time and space regardless of the size of the input | Accessing the Nth element of an Array, removing the first or last element of a List. |
| O(logN) | log, logarithmic | 1 -> log(100) = 2 | Binary search. |
| O(N log N) | n log n | 1 -> 100 x log(100) = 20 | Heapsort, merge sort. |
| O(N^2) | sqaured, quadratic | 1 -> 100^2 = 10 000 | 2 nested loops, bubble sort, insertion sort. Walking the whole array for each element in the array. |
| O(N^3) | n cubed | 1 -> 100^3 = 1 000 000 | 3 nested loops, |
| O(2^N) | exponential | 1 -> 1E27 | ... |
| O(N!) | factorial | 1 -> 3E151 | ... |
Array
The basic data structure is an array.
They can be thought of as a contiguous memory space, which has a defined length.
For example using Node.js you can create a raw binary data buffer and set its length in bytes, using ArrayBuffer
Here we create an buffer of a length of 8 bytes.
1const buffer = new ArrayBuffer(8);
2You can't directly write to that memory space. You need to create a typed array object which represents that raw binary buffer in a specific format. It sets the length of the elements of the array, which lets us then read and write to that array using the correct type.
Here we set the type of the array to unsigned 8 bits integers.
1const ua8 = new Uint8Array(buffer);
2It means that it will use 8 bits to store a integer, so the number stored can go from 0 to 255 - 255 being the highest number we can represent using 8 bits, as it's encoded as 11111111 in binary.
When we assign a number to an index of the array, it's positioned using 8 bit elements:
1ua8[2] = 42;
2buffer
3ArrayBuffer {
4 [Uint8Contents]: <00 00 2a 00 00 00 00 00>,
5 byteLength: 8
6}
7When in the same memory buffer we write to the same index 2, but using a array typed with 16 bits the value ends up being set on the byte of index 4 since we're using a type that has twice the size of the original 8 bit array:
1const ua16 = new Uint16Array(buffer);
2
3ua16[2] = 42;
4buffer
5ArrayBuffer {
6 [Uint8Contents]: <00 00 2a 00 00 00 00 00>,
7 byteLength: 8
8}
9On those basic arrays the big O of inserting, reading, and deleting are constant time because we are only accessing the values at know indexes and don't need to walk over the array. So one issue we have with those arrays is to find values in them. We're going to go over that with few different algorithm starting with linear search.
Linear search
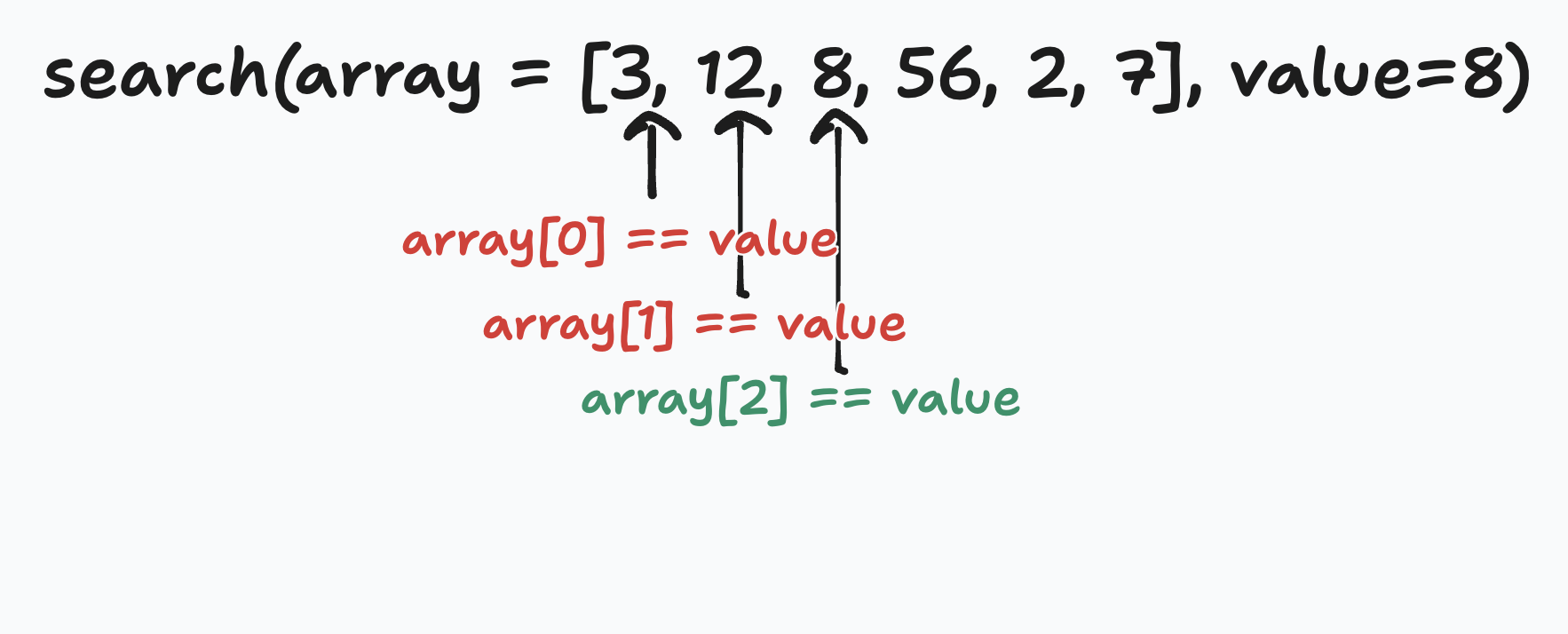
Linear search walks the array, comparing each elements to the value we are looking for, and returning the index of the element which the value matches.
The big O for that algorithm would be O(N) because it grows linearly with the size of the array. In other words, if it would take 1 second to find the value in an array of size 1, it would take 10 seconds in an array of size 10, and 100 seconds in an array of size 100.
Let's implement it!
1function linearSearch(
2 array: number[] | string[],
3 value: number
4): number | false {
5 for (let i = 0; i < array.length; i++) {
6 if (array[i] === value) {
7 return i;
8 }
9 }
10 return false;
11}
12We have a linearSearch function, that takes two parameters. The first one is an array of either strings or numbers, and the second one is the value we are looking for. We use a for loop to iterate over the array, and access each of its elements. We then return the index at which we found the value if the current element matche, or - after walking the whole array, which is the worst case - we end up returning false.
Binary search
Binary search works on sorted array, by jumping to a point in the array - usually in the middle - called the pivot point. We check wether that pivot point value is bigger or smaller than the value we are looking for. Taking advantage of the fact that the array is sorted, we now have divided the search space in two, and only have to search the part that possibly contains our value. If the pivot point is smaller than our value we continue to serch in the range container between the pivot point and the end of the array, while if it was bigger we'd keep on looking between the start of the array and our pivot point.
By keeping on splitting the search space in two we avoid having to walk any portion of the array until we've either found our value or made sure it's not present. We also avoid doing linear search, and improve the runtime.
Because we only have half of N steps at each iteration, the big O for that algorithm is log(N).
Let's look at a schema to understand how the algorithm works:
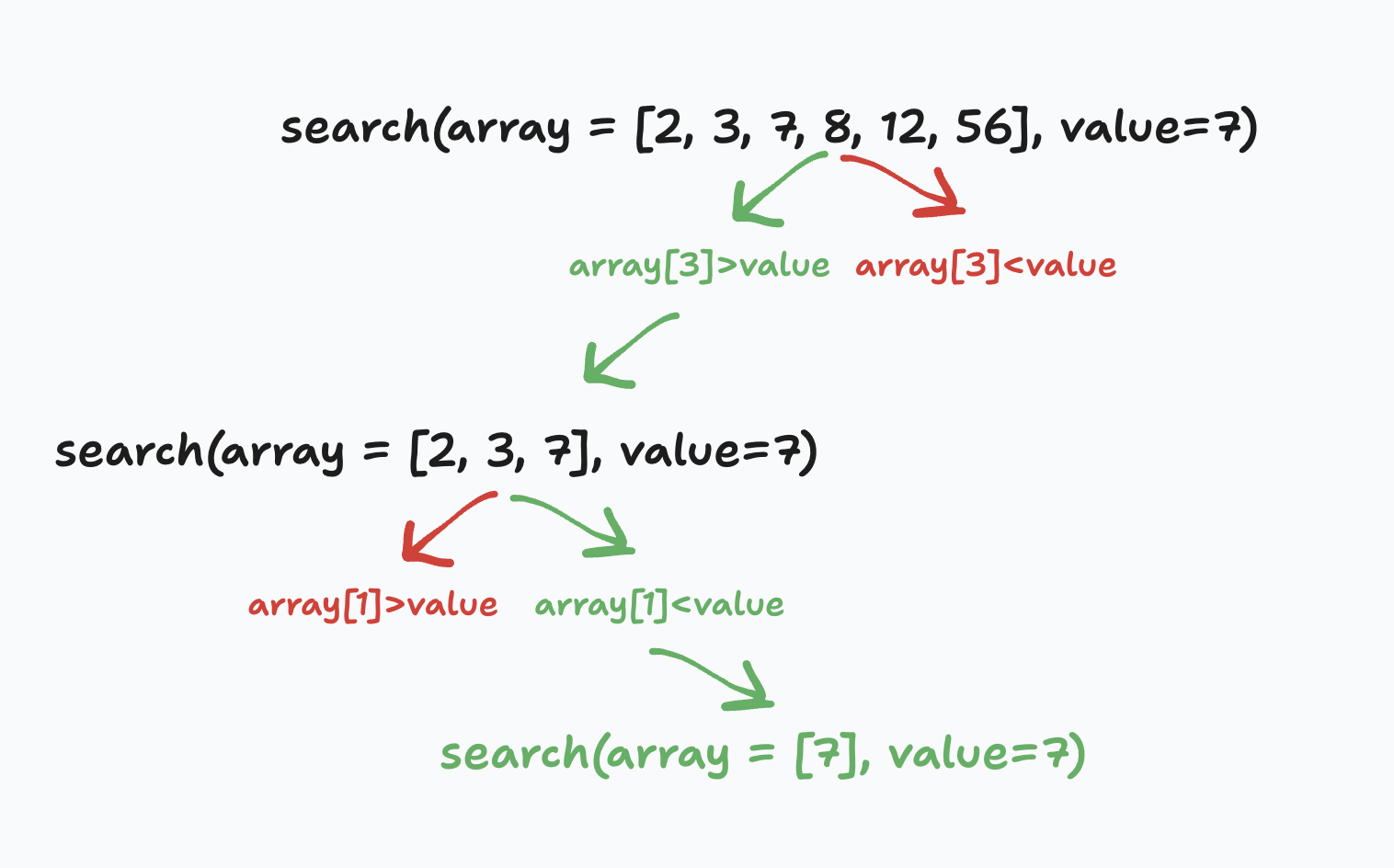
We can see in the schema how we divide the array in two every time, checking wether the middle value is larger or smaller than our search value, and continuing to split it further in two until found. This lends itself well to recursion, so let's implement it!
We start with a function that takes 4 parameters: the array we are searching in, the search value, and the low and high parameters are the indexes that start and end the array we are searching in.
These low and high will help us define the bounds of the array we will search in. Let's continue to describe the function, as these will make sense just a bit later.
For the first iteration the default low and high param are the original array min and max indexes.
We then start by checking wether our low and high indexes are the same. That would mean that we have an empty array, and haven't found our value, so we return false.
We then proceed to find the middle point of our array, and grab it's value. We'll compare it to our search value, and of course if it matches we'll return true.
If it doesn't match we then have two choices:
If our search value is bigger and because our array is sorted, we'll continue searching in the sub array to the right of our middle point. So we define our low as being the next element after our middle point, and call our search function again with an updated low param.
If our search value is smaller that the middle value, we'll continue searching in the sub array that precedes the middle point. We then keep our original low, but pass as the high param the middle point index.
This let us recurse, calling the function again with updated bounds for the sub-array, and we continue to search for our value in smaller and smaller sub-arrays until we hit one of our two exit conditions, having found or not our search value.
1export default function bs_list(
2 array: number[],
3 searchValue: number,
4 low: number = 0,
5 high: number = array.length
6): boolean {
7 if (low == high) {
8 return false;
9 }
10
11 const middle = Math.floor((low + high) / 2);
12 const currentValue = array[middle];
13
14 if (currentValue === searchValue) {
15 return true;
16 } else if (searchValue > currentValue) {
17 low = middle + 1;
18 return bs_list(array, searchValue, low, high);
19 } else {
20 high = middle;
21 return bs_list(array, searchValue, low, high);
22 }
23}
24